1.1 Cruzar puentes
Moore, Cristopher, and Mertens, Stephan. The Nature of Computation. United Kingdom, OUP Oxford, 2011. Capítulo 1. Traducción en español de Eduardo Alemán.
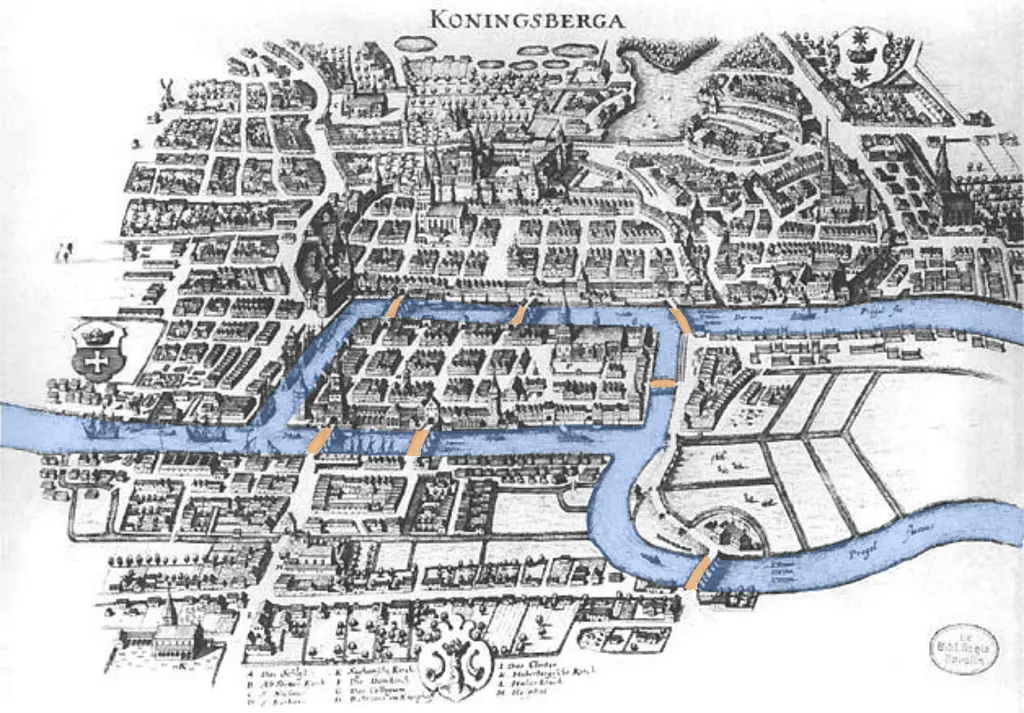
Comenzamos nuestro viaje hacia la naturaleza de la computación con un paseo por Königsberg (ahora Kaliningrado) del siglo XVIII. Como se puede ver en la Figura 1.1, la ciudad de Königsberg se extiende a ambos lados del río Pregel con siete puentes que conectan las dos orillas del río con dos islas. Un acertijo popular de la época preguntaba si se podía caminar por la ciudad de manera que se cruzara cada puente exactamente una vez.
Figura 1.1 La ciudad de Königsberg en el siglo XXVII.
Desconocemos el esfuerzo que los ciudadanos de Königsberg dedicaron a resolver este acertijo en sus paseos dominicales, pero sí sabemos que nunca lo lograron. Fue Leonhard Euler quien resolvió este enigma en 1736. Como matemático, Euler prefirió abordar el problema mediante el pensamiento puro en lugar de la experimentación. Reconoció que el problema depende únicamente del conjunto de conexiones entre las orillas del río y las islas: un grafo en términos modernos.
El grafo correspondiente a Königsberg tiene cuatro vértices que representan las dos riberas y las dos islas, y siete aristas que representan los puentes, como se muestra en la Figura 1.2. Hoy en día, decimos que un recorrido por un grafo que cruza cada arista una vez es un recorrido euleriano, o un ciclo euleriano si regresa a su punto de partida. Decimos que un grafo es euleriano si posee un ciclo euleriano.
Figura 1.2 Los siete puentes de Königsberg. A la izquierda, tal como se dibujaron en el artículo de Euler de 1736, y a la derecha, tal como se representan en un grafo en el que cada ribera o isla es un vértice y cada puente una arista.
Ahora que hemos reducido el problema a un grafo que podemos dibujar en una hoja de papel, es fácil explorar varios recorridos mediante prueba y error. Sin embargo, Euler se dio cuenta de que probar todos los recorridos posibles de esta manera llevaría tiempo. Como señaló en su artículo (traducido del latín):
En cuanto al problema de los siete puentes de Königsberg, se puede resolver elaborando una lista exhaustiva de posibles rutas y determinando si alguna satisface las condiciones del problema. Debido al número de posibilidades, este método de solución sería demasiado difícil y laborioso, y en otros problemas con más puentes, sería imposible.
Seamos más cuantitativos. Supongamos, para simplificar, que cada vez que llegamos a una isla o a la orilla de un río hay dos maneras diferentes de salir. Entonces, si hay número $n$ de puentes que cruzar, una estimación aproximada del número de posibles recorridos sería $2^n$. En el rompecabezas de Königsberg tenemos $n = 7$, y mientras que generar y verificar manualmente $2^7$ o 128 rutas tomaría bastante tiempo, una computadora moderna podría hacerlo en un instante.
Pero la observación de Euler no se refiere solo a los puentes de Königsberg. Se refiere a toda la familia de problemas de este tipo y a cómo su dificultad escala en función del número de puentes. Si consideramos los puentes de Venecia, donde $n = 420$, o los de Pittsburgh, donde $n = 446$, incluso la computadora más rápida imaginable tardaría más que la edad del universo en realizar una búsqueda exhaustiva.
Euler tuvo una ingeniosa idea que nos permite evitar esta búsqueda por completo. Observó que, para cruzar cada arista una vez, cada vez que llegamos a un vértice por una arista, debemos partir por una arista diferente. Por lo tanto, las aristas de cada vértice deben venir en pares, con una arista de “salida” por cada arista de “llegada”. De ello se deduce que el grado de cada vértice (el número de aristas que lo tocan) debe ser par, salvo para los vértices donde comienza y termina el recorrido, que pueden tener grado impar si no coinciden.
Esto demuestra que una condición necesaria para que un grafo sea euleriano es que todos sus vértices tengan grado par. Euler afirmó que esta condición también es suficiente y enunció el siguiente teorema:
Teorema 1.1
Un grafo conexo contiene un ciclo euleriano si y solo si cada vértice tiene grado par.
Si exactamente dos vértices tienen grado impar, contiene un recorrido euleriano, pero no un ciclo euleriano.
Este teorema nos permite resolver los puentes de Königsberg muy rápidamente. Como señala el poema que encabeza este capítulo, los cuatro vértices tienen grado impar, por lo que no existe un recorrido euleriano que atraviese el casco antiguo de Königsberg.
Más allá de resolver este problema, la idea de Euler marca una enorme diferencia en la escalabilidad del problema. Una búsqueda exhaustiva en una ciudad con $n$ puentes requiere un tiempo que crece exponencialmente con $n$. Pero podemos comprobar que cada vértice tiene grado par en un tiempo lineal, suponiendo que se nos proporciona el mapa de la ciudad en un formato conveniente.
Además de la aceleración del tiempo exponencial al lineal, la intuición de Euler transforma este problema de otra manera. ¿Qué se necesita para demostrar la existencia, o inexistencia, de un recorrido euleriano? Si existe, podemos demostrarlo simplemente mostrándolo. Pero si no existe, ¿cómo convencer a otros?
Imaginen que Euler hubiera usado fuerza bruta: presentar una lista completa de recorridos y mostrar que ninguno sirve. Muchos se habrían negado a revisarla y habrían sospechado que omitió una ruta. Una demostración así sería lógica, pero insatisfactoria: no explica por qué no existe una solución.
En cambio, el argumento de Euler es simple, conciso e irresistible: basta con mostrar tres vértices de grado impar. Así, Euler cambió la estructura lógica del problema y el tipo de evidencia que requiere: una demostración conceptual, no una lista interminable. Una verdadera revolución del pensamiento.
1.2 Itinerarios sin solución
El siguiente paso en nuestro viaje nos lleva a la Irlanda del siglo XIX y al Astrónomo Real, Sir William Rowan Hamilton, conocido por todos los físicos por sus contribuciones a la mecánica clásica. En 1859, Hamilton lanzó al mercado un nuevo rompecabezas, llamado el “juego icosiano”, que se muestra en la Figura 1.4. El juego fue un fracaso comercial, pero condujo a uno de los problemas más icónicos de la informática actual.
El objetivo del juego es recorrer las aristas de un dodecaedro visitando cada vértice una sola vez. En realidad, era un juego para dos jugadores en el que uno elige los primeros cinco vértices y el otro intenta completar el recorrido; pero por ahora, pensemos solo en la versión en solitario. Si bien estos recorridos se habían considerado en otros contextos, hoy los llamamos recorridos o ciclos hamiltonianos, y decimos que un grafo es hamiltoniano si posee un ciclo hamiltoniano. Uno de estos ciclos para el dodecaedro se muestra en la Figura 1.5.
Figura 1.5 A la izquierda, el dodecaedro; a la derecha, una versión aplanada del grafo formado por sus aristas. Un ciclo hamiltoniano, que visita cada vértice una vez y regresa a su punto de partida, se muestra en negrita.
Nota del traductor: Euler formuló el problema de la siguiente manera: “En la ciudad de Königsberg, en Prusia, hay una isla A llamada Kneiphof, rodeada por los dos brazos del río Pregel. Hay siete puentes a, b, c, d, e, f y g, que cruzan por los dos brazos del río. La cuestión consiste en determinar si una persona puede realizar un paseo de tal forma que cruce cada uno de estos puentes sólo una vez”.
…